

The moment of inertia I x I x about the x -axis x -axis for the region R R is the limit of the sum of moments of inertia of the regions R i j R i j about the x -axis. The moment of inertia is related to the rotation of the mass specifically, it measures the tendency of the mass to resist a change in rotational motion about an axis. ( x i j * ) 2 ρ ( x i j *, y i j * ) Δ A. Similarly, the moment of inertia of the subrectangle R i j R i j about the y -axis y -axis is ( x i j * ) 2 ρ ( x i j *, y i j * ) Δ A. ( y i j * ) 2 ρ ( x i j *, y i j * ) Δ A.
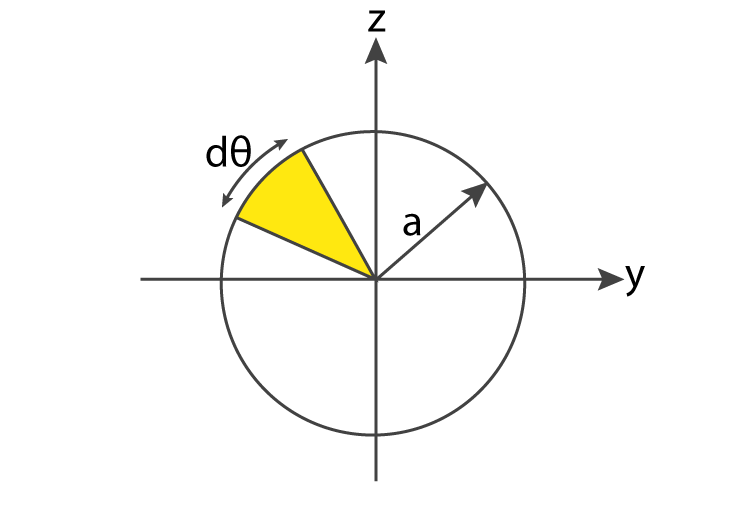
We can see from Figure 5.66 that the moment of inertia of the subrectangle R i j R i j about the x -axis x -axis is ( y i j * ) 2 ρ ( x i j *, y i j * ) Δ A.

The moment of inertia of a particle of mass m m about an axis is m r 2, m r 2, where r r is the distance of the particle from the axis.
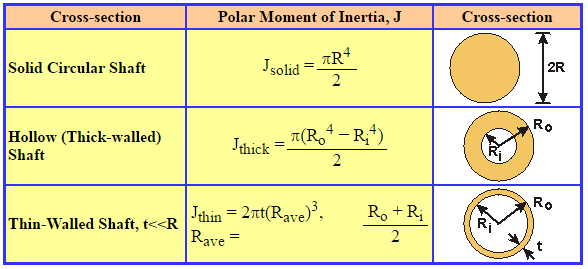
#Polar moment of inertia of a circle how to
Moments of Inertiaįor a clear understanding of how to calculate moments of inertia using double integrals, we need to go back to the general definition of moments and centers of mass in Section 6.6 of Volume 1. Ĭalculate the centroid of the region between the curves y = x y = x and y = x y = x with uniform density in the interval 0 ≤ x ≤ 1. x c = M y m = ∬ R x d A ∬ R d A and y c = M x m = ∬ R y d A ∬ R d A, x c = M y m = ∬ R x d A ∬ R d A = ∫ x = 1 x = 3 ∫ y = 0 y = e x x d y d x ∫ x = 1 x = 3 ∫ y = 0 y = e x d y d x = ∫ x = 1 x = 3 x e x d x ∫ x = 1 x = 3 e x d x = 2 e 3 e 3 − e = 2 e 2 e 2 − 1, y c = M x m = ∬ R y d A ∬ R d A = ∫ x = 1 x = 3 ∫ y = 0 y = e x y d y d x ∫ x = 1 x = 3 ∫ y = 0 y = e x d y d x = ∫ x = 1 x = 3 e 2 x 2 d x ∫ x = 1 x = 3 e x d x = 1 4 e 2 ( e 4 − 1 ) e ( e 2 − 1 ) = 1 4 e ( e 2 + 1 ). X c = M y m = ∬ R x d A ∬ R d A and y c = M x m = ∬ R y d A ∬ R d A, x c = M y m = ∬ R x d A ∬ R d A = ∫ x = 1 x = 3 ∫ y = 0 y = e x x d y d x ∫ x = 1 x = 3 ∫ y = 0 y = e x d y d x = ∫ x = 1 x = 3 x e x d x ∫ x = 1 x = 3 e x d x = 2 e 3 e 3 − e = 2 e 2 e 2 − 1, y c = M x m = ∬ R y d A ∬ R d A = ∫ x = 1 x = 3 ∫ y = 0 y = e x y d y d x ∫ x = 1 x = 3 ∫ y = 0 y = e x d y d x = ∫ x = 1 x = 3 e 2 x 2 d x ∫ x = 1 x = 3 e x d x = 1 4 e 2 ( e 4 − 1 ) e ( e 2 − 1 ) = 1 4 e ( e 2 + 1 ). The lamina is perfectly balanced about its center of mass. Figure 5.64 shows a point P P as the center of mass of a lamina. If the object has uniform density, the center of mass is the geometric center of the object, which is called the centroid. The center of mass is also known as the center of gravity if the object is in a uniform gravitational field. The density is usually considered to be a constant number when the lamina or the object is homogeneous that is, the object has uniform density. In this section we develop computational techniques for finding the center of mass and moments of inertia of several types of physical objects, using double integrals for a lamina (flat plate) and triple integrals for a three-dimensional object with variable density. We have already discussed a few applications of multiple integrals, such as finding areas, volumes, and the average value of a function over a bounded region. 5.6.3 Use triple integrals to locate the center of mass of a three-dimensional object.5.6.2 Use double integrals to find the moment of inertia of a two-dimensional object.


 0 kommentar(er)
0 kommentar(er)
